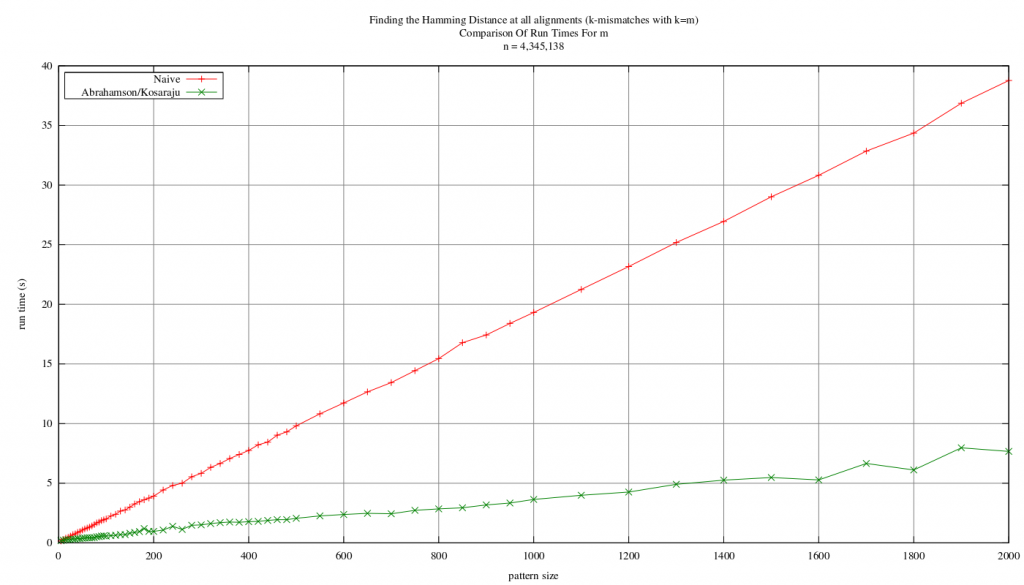
Until now I’d not run any tests comparing the two methods that can report the hamming distance at all alignments of text and pattern (A special case of k-mismatches where k >= m). The methods are the naive approach and the algorithm of Abrahamson/Kosaraju which runs in
. Early results are quite pleasing though! The following shows a graph of run-times for varying pattern sizes with a text size of 4,345,138 (the full length of the source). The text and pattern were taken from an English text sourced from Project Gutenberg:
It’s a little hard to see down at the lower pattern sizes (in fact it’s pretty hard to see at all unless you click for a larger version!), but the Abrahamson/Kosaraju method is faster right down to pattern sizes of about 5! It’s interesting to see that there are some slight bumps in the run time of the algorithm; though this can be attributed to the number of “frequent” characters — for each frequent character matching is done using FFTs, which adds some overhead. It’s further complicated by the fact that a character which occurs only just enough times to be considered frequent will have more relative overhead than a character which is far above the “frequent threshold” — in each case we’ll do the same amount of work, but in the latter case, we should see less use of the “counting” part of the algorithm.
I’ll run some tests on larger text sizes over night and also use some different sources; it’ll be interesting to see how it fares with a smaller alphabet size, perhaps using the DNA corpus from Pizza and Chili