So I’ve spent most of the day fixing a few bugs and dealing with some edge cases. That’s the nice thing about theory: you can ignore all the slight caveats and small problems. The two problems today have been: 1.) rounding of the values of — I ran into a problem because I was rounding down, resulting in it not being possible to find enough matches for a given alignment to surpass the threshold at which potential mis-matches are verified with LCEs and 2.) producing p-representations when not all of the characters in the text are in the pattern — to deal with this we change the last character of the pattern to some special character and set all characters that don’t occur in the pattern to this character as well. You have to be careful if the only occurrence of a character in the pattern is the last character though!
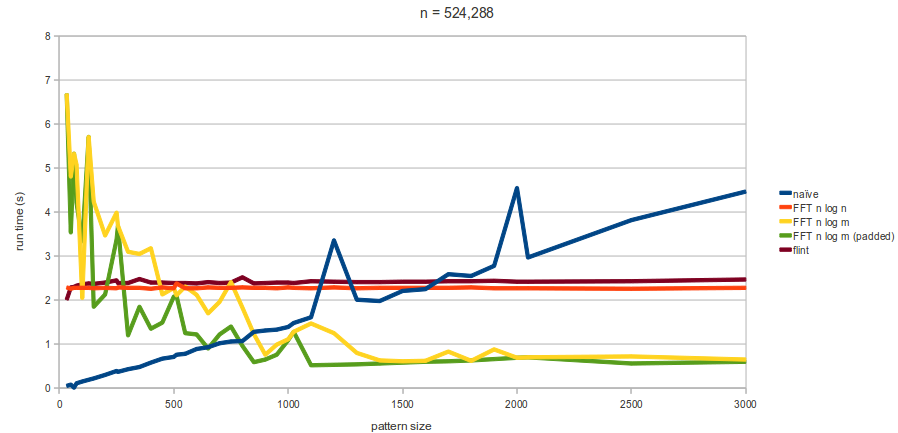
On a more positive note, some tests that enforce the worst case for the naive method (text and pattern are both mostly a’s with the necessary number of b’s at the end to ensure a k-mismatch only occurs right at the end) have shown that all the methods are faster even for pretty small pattern sizes. With a text size of 1,000,000, the method is faster from pattern sizes greater than 30 or so. Interestingly, at these small pattern sizes the
is running at least 1.5x as slow as this, even if we exclude the pre-processing time and use a very small k. This contradicts what I was looking at yesterday, though I suspect those times may be have been a bit skewed by a couple of bugs.
Perhaps for larger pattern sizes we’ll see the latter method performing better.